Hello guys,
I have to design an integrator circuit using an op-amp for my simulation lab assignment.

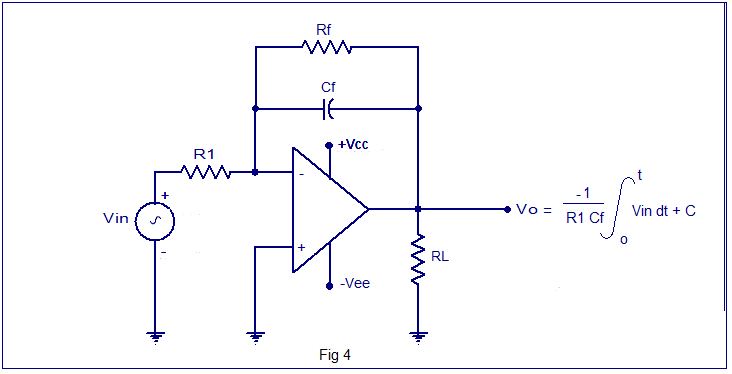
my first question is, how do i deal with that constant C?

my second question is, what should be the order of magnitude of my resistance R1, Rf and my capacitance Cf if my sinusoidal input peak voltage is 1V and i want my output peak voltage to be 1V?

 

What you have depicted isn't an integrator - it's an active low pass filter.

Before I help with homework/lab assignments I ask the user to make an attempt at answering their own question.

 

An integrator is a low pass filter.

 

C is the initial voltage (if any) on the capacitor.

Rf is typically used with an op amp integrator to minimize drift and offset from the op amp voltage and current offsets. It's value is high enough so it doesn't significantly affect the highest frequencies you want to integrate (its resistance is high compared to the capacitance reactance at that frequency).

The rest you should be able to calculate from the integrator equations.

Hint: For sinusoidal input you might want to use the frequency domain equations rather than the time domain.

 

An integrator is a low pass filter.

Well, yes - technically - I guess I hadn't really thought of it in this manner.

What I was trying to say was that this circuit won't give you the integral of the input that is readily apparent, as the OP states. Of course this will integrate at frequencies above the knee (this is what I hadn't really thought of before). Frequencies below the knee will have a completely different characteristic. The OP suggests that the integral is simply the integral of the output, but that is only true above the knee.

The actual integral (I'm still trying to figure out how this simplifies - it's late and my brain shut off).
\(v_{out}(t)=\frac{-1}{R_{1}C_{f}}\int^{t}_{0}v_{in}(t-\tau)e^{-\tau/(R_{f}C_{f})}d\tau\)

edit: Oh, and thanks - I learned something new today!

 

What you have depicted isn't an integrator - it's an active low pass filter.

Before I help with homework/lab assignments I ask the user to make an attempt at answering their own question.

Actually simulators are weird and not at all perfect. Suppose for an example, i have an inverting amplifier. Its gain is defined by -Rf/R1. If I use values Rf = 2 ohm and R1 = 1 ohm, then I will get a signal whose amplitude is twice to the input signal but vertically inverted.

Now for the practical consideration 1 ohm and 2 ohm resistance are not appropriate. That is why i asked how large my resistance value should be. Simulator components don't break but the real components do break.

 

C is the initial voltage (if any) on the capacitor.

Rf is typically used with an op amp integrator to minimize drift and offset from the op amp voltage and current offsets. It's value is high enough so it doesn't significantly affect the highest frequencies you want to integrate (its resistance is high compared to the capacitance reactance at that frequency).

The rest you should be able to calculate from the integrator equations.

Hint: For sinusoidal input you might want to use the frequency domain equations rather than the time domain.

Thanks. that was a great help.

 

Actually simulators are weird and not at all perfect. Suppose for an example, i have an inverting amplifier. Its gain is defined by -Rf/R1. If I use values Rf = 2 ohm and R1 = 1 ohm, then I will get a signal whose amplitude is twice to the input signal but vertically inverted.

Now for the practical consideration 1 ohm and 2 ohm resistance are not appropriate. That is why i asked how large my resistance value should be. Simulator components don't break but the real components do break.

Yes - but your simulator should simulate the amount of power you're using in your opamp and resistors. The simulator (ltspice/pspice) leaves it to the user to size their parts appropriately. It assumes perfect parts (power-wise). It's the power disipated that will break your parts. If you have large enough 2ohm and 1ohm resistors and a opamp that will source/sink the specified amount of current, then theoretically the 2ohm and 1ohm resistors should work. Although you'll probably run into other issues (loading effects?) with such low resistances.

As a rule of thumb - 1/8W resistors in the few kohm range is adequate for low power applications (such as an op-amp integrator), but do the math for your application!